¿Alguna vez te has preguntado cuál es la tecnología que protege tus emails o mantiene segura tu navegación por Internet? En el corazón de la criptografía moderna existe un algoritmo conocido como Diffie-Hellman que sustenta el intercambio de mensajes de forma segura.
Si quieres enterarte de cómo funciona este algoritmo, continúa leyendo.
¿Qué es el algoritmo Diffie-Hellman?
El algoritmo de Diffie-Hellman es un protocolo criptográfico diseñado para el intercambio seguro de claves criptográficas sobre un canal de comunicación público y no seguro. Este algoritmo permite que dos partes que no tienen conocimiento previo entre sí, generen de manera conjunta una clave secreta compartida. De esa forma, ayuda a cifrar y descifrar mensajes.
El algoritmo se fundamenta en la dificultad computacional del problema del logaritmo discreto en grupos cíclicos. ¿Qué significa esto? Pues que aunque el canal público implica el intercambio de valores derivados de las claves secretas, calcular la clave compartida sin tener acceso a una de las claves privadas resulta inviable con la tecnología actual.
¿Cómo surge el algoritmo de Whitfiel Diffie y Martin Hellman?
Hasta la década de 1970, la criptografía de claves simétricas dominaba, limitada por la necesidad de compartir una clave secreta de manera segura antes de poder establecer comunicaciones seguras.
Este paradigma cambió radicalmente con el trabajo seminal de Whitfield Diffie y Martin Hellman.

La publicación de «New Directions in Cryptography» en 1976 introdujo el algoritmo de Diffie-Hellman y sentó las bases de la criptografía asimétrica. El trabajo se inspiró en los «rompecabezas de Merkle», un precursor crítico que, aunque más rudimentario, apuntaba hacia la posibilidad de compartir claves secretas sin un intercambio directo.
Dentro de este contexto histórico, es crucial reconocer el entorno de innovación y colaboración que permitió el salto conceptual hacia la criptografía de clave pública. A diferencia de los sistemas de cifrado simétrico donde la misma clave cifra y descifra el mensaje, el algoritmo de Diffie-Hellman implementa un enfoque asimétrico donde dos partes pueden generar una clave compartida de forma independiente, utilizando sus claves privadas y públicas sin revelarlas directamente entre sí.
La contribución de Diffie y Hellman allanó el camino para el desarrollo de sistemas de criptografía asimétrica completos, como RSA, que surgiría poco después. Sin embargo, la historia del algoritmo de Diffie-Hellman y la criptografía de clave pública tiene una capa adicional de complejidad.
En 1997, se desclasificaron documentos del GCHQ que revelaban que James Ellis había concebido la idea de la criptografía de clave pública en la década de 1960. Por otro lado también se descubrió que Clifford Cocks y Malcolm Williamson habían desarrollado un algoritmo equivalente al RSA y al algoritmo de Diffie-Hellman, respectivamente, varios años antes de que estos fueran conocidos públicamente.
Sin embargo, debido a su clasificación, estos avances no influyeron en la comunidad criptográfica más amplia hasta mucho después.
¿Diffie-Hellman es un algoritmo de cifrado?
Antes de continuar con nuestro artículo, y proceder a su aplicación y funcionamiento, debemos hacer una aclaración clave: Diffie-Hellman NO es un algoritmo de cifrado.
A menudo, existe confusión respecto a este tema, ya que su uso está intrínsecamente relacionado con el cifrado de comunicaciones. Sin embargo, es crucial entender que Diffie-Hellman se especializa en el intercambio de claves de manera segura a través de un canal inseguro, sin involucrarse directamente en el cifrado o descifrado de los mensajes.
Algoritmo de Diffie-Hellman ¿dónde se utiliza?
El protocolo Diffie Hellman se despliega en una variedad de escenarios críticos.
Por ejemplo, cuando navegas por Internet y ves el candado de seguridad al lado de la URL de un sitio web, hay una buena probabilidad de que el algoritmo Diffie-Hellman esté trabajando para proteger tu conexión mediante TLS (Transport Layer Security). Esta tecnología crea un túnel cifrado entre tu navegador y el servidor web, permitiendo que la información sensible, como los detalles de tu tarjeta de crédito, se transmita de forma segura.
Más allá de la web, el algoritmo de Diffie-Hellman se emplea en SSH (Secure Shell), un protocolo que proporciona un método seguro para acceder a computadoras remotas. Aquí, facilita un intercambio de claves que permite que la sesión remota se cifre, asegurando que los comandos y la información transmitida permanezcan inaccesibles para los observadores no deseados.
En el ámbito del correo electrónico, el algoritmo Diffie-Hellman, junto con PGP (Pretty Good Privacy), proporciona una capa de cifrado para los mensajes, asegurando que solo el receptor pueda leer el contenido del correo.
Además, el algoritmo de Diffie-Hellman se extiende a IPsec, un conjunto de protocolos utilizado para proteger el tráfico de Internet en la capa de red.
¿Cómo funciona el algoritmo de Diffie-Hellman?
Para entender el funcionamiento del algoritmo de Diffie- Hellman, vamos a desglosarlo en dos casos. Uno teórico y uno práctico.
Empecemos por la teoría:
1. Acuerdo de parámetros públicos
- Selección de un Número Primo Grande (p): Se elige un número primo grande p, que será conocido por ambas partes y por cualquier observador potencial. Este número sirve como el módulo para las operaciones subsiguientes.
- Selección de la Base (g): Se acuerda una base g, que es una raíz primitiva módulo p. La base g es un número entero menor que p y también es pública.
2. Generación y envío de claves públicas
- Generación de la Clave Privada de la Parte 1: La primera parte selecciona un número secreto a, que sirve como su clave privada. Este número no se comparte con nadie.
- Cálculo de la Clave Pública de la Parte 1: La clave pública A se calcula utilizando la fórmula A=gᵃ mod p y luego se envía a la segunda parte.
- Generación de la Clave Privada de la Parte 2: La segunda parte selecciona su número secreto b, que actúa como su clave privada.
- Cálculo de la Clave Pública de la Parte 2: La clave pública B se calcula como B=gᵇ mod p y se envía a la primera parte.
3. Generación de la clave compartida
- Cálculo de la Clave Compartida por la Parte 1: Utilizando la clave pública recibida de la segunda parte (B), la primera parte calcula la clave compartida s usando su clave privada (a) mediante la fórmula s=Bᵃ mod p
- Cálculo de la Clave Compartida por la Parte 2: De manera similar, la segunda parte utiliza la clave pública recibida de la primera parte (A) y su clave privada (b) para calcular la clave compartida s como s=Aᵇ mod p
Ambas partes llegan de manera independiente al mismo valor de s, que ahora pueden utilizar como una clave secreta compartida para cifrar la comunicación.
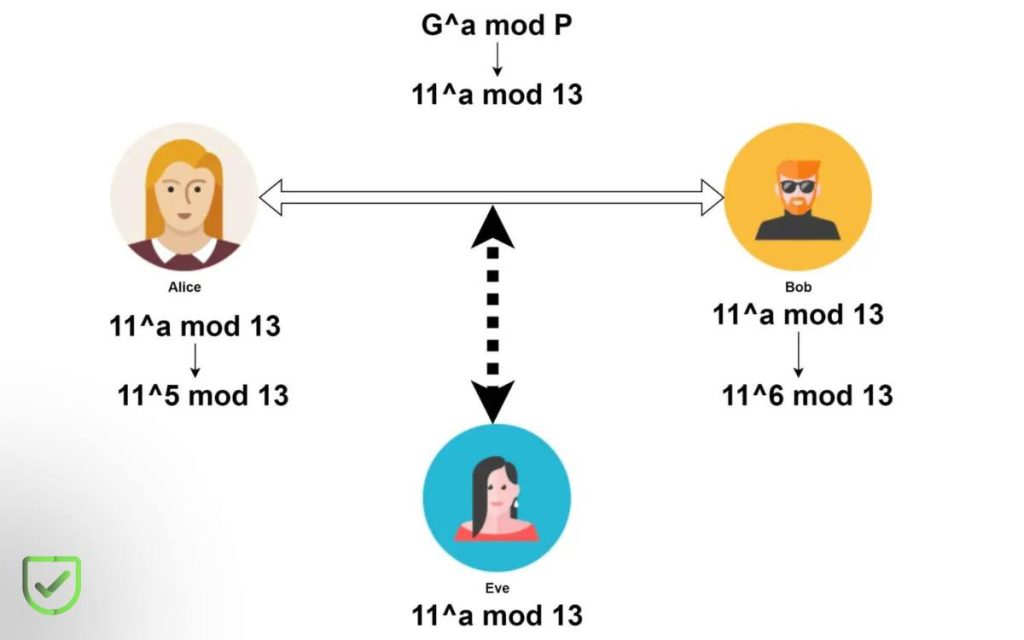
Funcionamiento del algoritmo Diffie-Hellman: Ejemplo
Ahora, veamos este mismo funcionamiento pero un caso práctico.
Imagina que Alice y Bob quieren compartir un secreto para abrir un candado que protege una caja de tesoros, pero quieren hacerlo sin que Eve, que está espiando, pueda descubrir ese secreto.
Paso 1: Acuerdo de colores básicos
Primero, Alice y Bob acuerdan públicamente en usar un color base, digamos amarillo, como punto de partida. Este color es conocido por todos, incluida Eve, la espía.
En términos técnicos, este color base es similar a seleccionar un número primo grande p y una base g en el algoritmo de Diffie-Hellman.
Paso 2: Selección de colores secretos
Luego, Alice y Bob eligen un color secreto que no le dicen a nadie. Alice elige rojo y Bob elige azul.
En el mundo de la criptografía, esto sería equivalente a Alice y Bob eligiendo sus números secretos, a y b, respectivamente.
Paso 3: Mezcla de Colores «públicos»
Alice mezcla su color secreto rojo con el amarillo para obtener naranja, y Bob mezcla su azul secreto con el amarillo para obtener verde. Luego, se intercambian los colores resultantes públicamente.
Eve ve tanto el naranja como el verde, pero no puede determinar el color secreto original de Alice o Bob.
Paso 4: Creación del color secreto compartido
Cuando Alice recibe el verde de Bob, ella mezcla su color secreto rojo con él, resultando en un color marrón oscuro específico. Bob hace lo mismo con el naranja que recibió de Alice, mezclando su color secreto azul con él, y también obtiene exactamente el mismo marrón oscuro.
Ahora, Alice y Bob pueden usar su marrón oscuro compartido para abrir el candado. Mientras, Eve, a pesar de haber visto el amarillo, el naranja, y el verde, no puede deducir el marrón oscuro sin conocer los colores secretos originales de Alice y Bob.
Conclusión
El algoritmo de Diffie-Hellman se mantiene como un baluarte en el campo de la criptografía, demostrando que la genialidad en diseño puede trascender décadas de avances tecnológicos. Siendo la base de muchos de los métodos de seguridad que utilizamos actualmente.







